작성자: 장재혁, GIST 블록체인 인터넷 경제 연구센터 (센터장 이흥노)
This work was created through a joint research with Onther Co., LTD., and supported by a grant-in-aid of Institute of Information & Communications Technology Planning & Evaluation (IITP), Republic of Korea.
이 글은 정보통신기획평가원(IITP)의 지원을 받아 (주)온더와의 공동연구를 통해 만들어진 결과물이다.
※ 주의: Modular arithmetic (나머지 연산)에 관한 기초지식이 필요함
Schnorr 프로토콜은 대표적이며 단순한 대화형 영지식 증명 프로토콜이다. 증명하고자 하는 명제는 “공개된 값 \(y\)와 공개된 값 \(g\in F_p^*\)에 대하여1, \(y=g^x\bmod p\)을 만족시는 비공개 값 \(x\) (\(0\le x<p-1\))를 알고 있음”을 납득시키는 상황이다. 여기서\(p\)는 공개된 값이며 소수(prime number)이다. 그리고 \(g\)는 \(F_p\)의 primitive element2이다. 이 글에서 다룰 Schnorr프로토콜은 다음과 같다:
| 프로토콜 1. Schnorr 프로토콜 |
|---|
| 1. 증명자는 하나의 (비공개) 무작위 값 \(v\) \(\left( 0\le v<p-1 \right)\)로 \(t=g^v\bmod p\)를 계산 하여 검증자에게 보낸다. 2. 도전적 문제: 검증자는 하나의 무작위 값 \(c\) \(\left( 0<c<p-1 \right)\)를 증명자에게 보낸다. 3. 증명자는 \(r=v-cx\bmod \left( p-1 \right)\)를 계산하여 검증자에게 보낸다. 4. 검증자는 \(t\equiv g^ry^c\bmod p\)임을 확인한다. |
프로토콜 1에서, 증명자는 검증자에게 \(x\)를 직접적으로 전송 하지 않는다. \(x\)를 사용한 계산 결과 \(r\)을 전송하긴 하지만, \(r\)로부터 \(x\)를 알아내는 것은 매우 어렵다. 그럼에도 불구하고 검증자는 \(t\equiv g^ry^c\bmod p\)를 계산함으로써 증명자가 올바른 \(x\)를 사용하였는지 확인 할 수 있다. 다음의 분석을 통해 그 이유를 설명하겠다.
Schnorr 프로토콜의 영지식증명 성능 분석
위 프로토콜 1이 영지식 증명의 정의를 만족하는지를 확인하면 다음과 같다.
Q. (완전성) 만약 증명자가 \(x\)를 알고있다면, 검증자는 \(t\equiv g^ry^c\bmod p\)를 확인함으로써 이를 납득할 수 있는가?
A. 그렇다.
만약 증명자가 과정 3)에서 \(r\)을 계산 할 때 사용한 값 \(x\)가 \(y=g^x\bmod p\)를 만족시킨다면, \(g^ry^c\equiv g^v-cx\bmod \left( p-1 \right)g^cx\bmod p\)이다. Fermat’s little theorem3에 의해, \(g^cx\equiv g^cx\bmod \left( p-1 \right)\bmod p\)이고, 따라서 \(g^ry^c\equiv g^v\equiv t\bmod p\)이다.
Q. (건실성) 만약 거짓 증명자가 \(x\)를 모른다면, 프로토콜을 1회 실행함으로써 검증자에게 \(t\equiv g^ry^c\bmod p\)임을 납득시킬 수 있는가?
A. 그럴 수 없다.
거짓 증명자가 주장하는 값을 \(x'\)라 하자. 여기서 \(x'\ne x\)이다. 거짓 증명자가 검증자를 속이기 위해 목표하는 바는 합동방정식 \(t\equiv g^{r'}y^c\bmod p\)를 만족시키는 값 \(r'\)을 찾는것이다. 여기서 \(y^c\)와 \(t\)의 값은 고정되어 있으며 증명자에게 알려져 있으므로, 결국 증명자가 풀어야 할 합동방정식은 \(\left( y^c \right)^{-1} t\equiv g^{r'}\bmod p\)를 만족시키는 값 \(r'\)을 찾는 것 이다. 즉, 프로토콜 1의 과정 3)의 계산을 무시하고, 이 합동방적식의 해를 찾아 검증자에게 건네야 한다.
증명자가 풀어야 할 문제는 discrete logarithm 문제이다. 이는 logarithm 연산을 유한 체에서 수행하는 것으로, 실수 집합에서 수행 할 때 보다 계산이 훨씬 어렵다. 거짓 증명자가 택할 수 있는 다른 방법은 \(F_p-1\)의 원소들 중 무작위로 \(r'\)를 선택하여 그 값이 조건을 만족하는지 확인 하는 것이다. 한번 무작위 값을 선택하여 조건이 달성 될 확률은 \(\left( p-1 \right)^-1\)이다. 일반적으로 \(p\)는 아주 큰 숫자이므로, 거짓 증명자가 검증자를 납득시킬 확률은 아주 작다.
Q. (약한 영지식성) 프로토콜 실행을 1회 요청함으로써 검증자는 \(r\)로부터 \(x\)를 알아 낼 수 있는가?
A. 그럴 수 없다.
검증자가 건네받는 \(r=v-cx\bmod \left( p-1 \right)\)에서, 검증자가 알고 있는 값은 \(r\), \(p\), \(c\), 그리고 알지 못하는 값은 \(v\)와4 \(x\)이다. 탈취함수를 \(f:F_p-1\times F_p-1\to F_p-1\), 여기서 \(f\left( v',x' \right)=v'-cx'\bmod \left( p-1 \right)\)이라 정의하겠다. 검증자가 \(x\)를 알아내는 행위는 \(f^-1\left( r \right)\)의 원소를 찾는것과 동등하다. 그러나 함수 \(f\)의 정의역의 원소의 개수는 \(\left( p-1 \right)^2\)이고 공역의 원소의 개수는 \(p-1\)이기 때문에, 함수 \(f\)는 injective이다. 즉, inverse image \(f^-1\left( r \right)\)의 원소는 유일하지 않다. 검증자는 더 이상의 다른 정보가 없기 때문에 \(r\)로부터 \(x\)를 알아 낼 수 없다.
Q. (강한 영지식성) 프로토콜 실행을 다회 요청함으로써 검증자는 \(r\)로부터 \(x\)를 알아 낼 수 있는가?
A. 가능하다.
검증자가 증명자에게 프로토콜 실행을 다회 재요청함으로써 \(r\)로부터 \(x\)를 알아 내는 다양한 방법이 존재 할 수 있다. 그 중 한가지 예를 들겠다. 프로토콜을 \(i\)번째 실행 하였을 때 프로토톨상에서 생성된 비공개 값을 \(v_i\), 공개된 값들을 \(r_i\), \(c_i\), \(t_i\)라 하겠다. 같은 증명자가 반복 실행하므로, 비공개 값 \(x\)는 변하지 않음을 가정한다. 다음의 알고리즘 2는 프로토콜 1을 반복 실행하여 검증자가 증명자의 비공개 정보를 탈취하는 알고리즘이다:
| 알고리즘 2 . Schnorr 프로토콜에 사용 될 수 있는 비공개 정보 탈취 알고리즘 |
|---|
| 1. 검증자는 매 \(i\)번째 실행마다 증명자로부터 건네받은 \(\left( t_i,r_i,c_i \right)\)쌍을 저장해 둔다. 2. 매 실행이 끝날 때 마다, 자신이 저장해 놓은 데이터로부터 \(t_it_j\equiv 1\bmod p\) 이거나 혹은 \(t_i\equiv t_j\bmod p\)이 되도록 하는 서로다른 index 쌍 \(i,j\)가 존재하는지 확인하고, 만약 존재한다면 프로토콜 재실행 요청을 멈춘다. 3. 만약 \(t_it_j\equiv 1\bmod p\)라면, \(v_i+v_j\equiv 0\bmod \left( p-1 \right)\)이고, 따라서 \(x=-\left( r_i+r_j \right)\left( c_i+c_j \right)^-1\bmod \left( p-1 \right)\)이다. 4. 만약 \(t_i\equiv t_j\bmod p\)라면, \(v_i\equiv v_j\bmod \left( p-1 \right)\)이고, 따라서 \(x=\left( r_i-r_j \right)\left( c_j-c_i \right)^-1\bmod \left( p-1 \right)\)이다. |
프로토콜 1에서의 정의에 의해 \(t_i\equiv g^v_i\bmod p\) 이므로, 알고리즘 2는 결국 이전 실행에서 증명자가 선택했던 값 \(v_i\)와 일치하는 (혹은 그것의 additive inverse와 일치하는 \(v_j\)) 값이 다음 실행에서 선택될 때 까지 재실행이 요청되는 것이 핵심이다. 다시 말해, 과정 2의 조건이 만족되면 검증자는 비공개 정보를 탈취할 수 있다. 검증자가 비공개 정보를 탈취 할 빈도를 Monte carlo test를 통해 아래 그림 4과 같이 실험적으로 얻었으며, 그림 5는 이론적으로 계산된 확률이다.
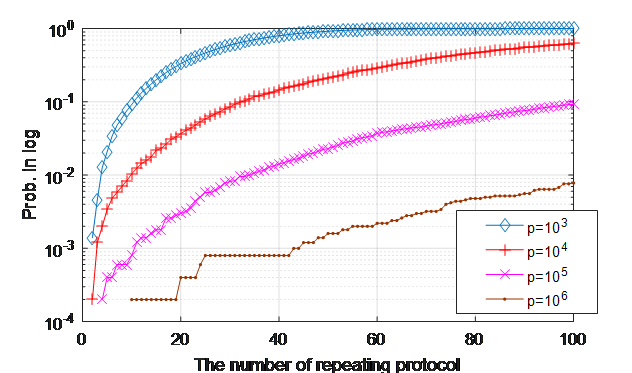 그림 4 실험적으로 얻은 검증자가 비공개 정보 탈취에 성공 할 실험적 확률. 가로축은 증명자에게 프로토콜 재실행을 요청하는 횟수이며, 세로축은 비공개 정보를 탈취 할 확률이다.
그림 4 실험적으로 얻은 검증자가 비공개 정보 탈취에 성공 할 실험적 확률. 가로축은 증명자에게 프로토콜 재실행을 요청하는 횟수이며, 세로축은 비공개 정보를 탈취 할 확률이다.
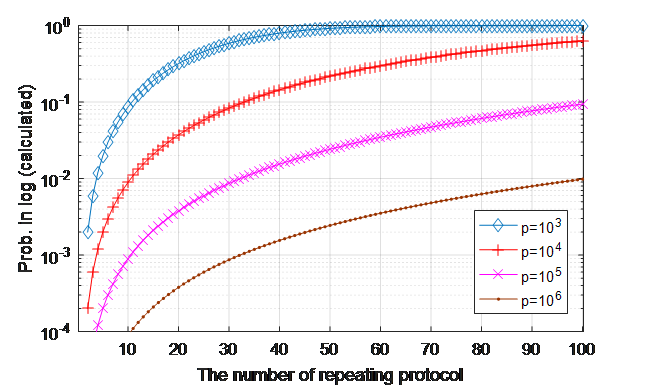 그림 5 계산으로 얻은 검증자가 비공개 정보 탈취에 성공 할 이론적 확률. 가로축은 증명자에게 프로토콜 재실행을 요청하는 횟수이며, 세로축은 비공개 정보를 탈취 할 확률이다.
그림 5 계산으로 얻은 검증자가 비공개 정보 탈취에 성공 할 이론적 확률. 가로축은 증명자에게 프로토콜 재실행을 요청하는 횟수이며, 세로축은 비공개 정보를 탈취 할 확률이다.
그림 5의 정보 탈취 확률이 무시할 수 없는 수준이라는 것을 더 직관적으로 확인하기 위해, \(y=g^x\bmod p\)의 discrete logarithm 문제를 직접 풀어 정보를 탈취 할 확률과 비교 할 수 있다. \(y\equiv g^x\bmod p\)의 해인 \(x\)를 찾을 확률은 아무 숫자 하나를 골라서 당첨 될 확률로 \(\left( p-1 \right)^-1\)이다. 이보다 1000배 더 큰 \(1000\left( p-1 \right)^-1\)의 확률로 정보를 탈취하기위해 필요로 하는 최소한의 프로토콜 재실행 횟수는 표 2와 같다. 표 2에 의하면, \(p\)의 값이 아무리 크더라도, 프로토콜을 약 33회 정도만 반복실행 하는 것을 통해 정보를 탈취 할 확률이 아무 숫자 하나를 골라서 당첨 될 확률보다 1000배 더 크다는 것을 알 수 있다.
| \(p\) | \(10^3\) | \(10^4\) | \(10^5\) | \(10^6\) | \(\cdots\) | \(10^10\) |
|---|---|---|---|---|---|---|
| 정보 탈취확률 | 1 | \(10^-1\) | \(10^-2\) | \(10^-3\) | \(\cdots\) | \(10^-7\) |
| 최소 프로토콜 재실행 횟수 | 182 | 33 | 33 | 33 | \(\cdots\) | 33 |
표 검증자가 \(1000\left( p-1 \right)^-1\)의 확률로 정보를 탈취하기위해 필요로 하는 최소한의 프로토콜 재실행 횟수. \(p\)의 크기가 1000근처의 수준인 경우, 검증자는 프로토콜을 약 182번 재실행하면 100%의 확률로 비공개 정보를 탈취 할 수 있다.
프로토콜 1이 강한 영지식성을 가지는 지를 명확히 결론내긴 어렵다. 프로토콜을 활용하는 환경에 따라 정보 탈취확률의 중요도가 다르기 때문이다. 예를 들어, \(p\)의 크기가 매우 크고 검증자가 증명자에게 프로토콜의 재실행을 요청할 수 있는 횟수가 제한된 환경이라면, 정보탈취확률은 무시할 수 있을 정도로 작을 것이다. 반면, 네트워크 환경이 불안정하여 프로토콜의 재실행 요청이 불가피한 환경이라면, 악의적 검증자가 정보탈취를 시도 할 가능성을 배제 할 수도 없다.
참고) 검증자가 \(n\)번째 재실행 요청 내에 비공개 정보 탈취에 성공 할 확률 \(P_n\):
짝수 \(p\)에 대하여, \(P_n = 1 - \begin{pmatrix} \frac{p-2}{2} \\ n \end{pmatrix} \frac{n!}{ ( ( p-2 ) / 2 )^2} \text{ for 0} \le n \le \frac{p-2}{2}\) 홀수 \(p\)에 대하여,
\[P_n = 1 - \left( \frac{p-3}{p-2} \right)^n \begin{pmatrix} \frac{p-3}{2} \\ n \end{pmatrix} \frac {n!}{ \left( \left( p-3 \right) / 2 \right)^n} - \frac { n \left( p-3 \right)^{n-1}}{ \left( p - 2 \right)^n} \begin{pmatrix} \frac{p-3}{2} \\ n-1 \end{pmatrix} \frac{ \left( n-1 \right) ! }{\left( \left( p - 3 \right) / 2 \right)^{n-1}} \text{ for 0} \le n \le \frac{p-3}{2}\]정리 1. 대화형 구조와 도전적 문제(challenge)의 필요성: 건실성 확보
프로토콜 1이 강한 건실성을 만족하는 이유는 도전적 문제에 해당하는 과정 2)의 존재 때문이다. 만약 과정 2)에서 검증자가 아닌 증명자가 임의로 값 \(c\)를 선택한다면, 거짓 증명자가 검증자를 기만 할 수 있다. 구체적으로, 거짓 증명자가 임의로 값 \(c\)와 \(r\)을 미리 선택한 후, \(t=g^ry^c\bmod p\)를 계산하여 과정 1)을 대체한다. 이후 과정 2)와 3)에서 미리 선택해둔 \(c\)와 \(r\)을 검증자에게 건넨다. 마지막으로 검증자는 과정 4)를 수행하면 검증이 완료된다. 결과적으로, 거짓 증명자는 \(x\)를 알지 못하여도 검증자를 기만 할 수 있게 된다.
과정 2)의 도전적 문제를 검증자가 직접 제출하더라도, 만약 과정 1)과 순서가 바뀌면 위와 같은 이유로 거짓 증명자가 검증자를 기만 할 수 있다. 따라서 프로토콜 1과 같이 과정 1)을 통해 증명자가 먼저 값 \(t\)를 제출 하게 한 후, 검증자는 이를 확인하고 도전적 문제 \(c\)를 제출하는 방식의 대화형 구조가 반드시 필요하다.
정리 2. 과정 1) (임의의 값 \(v\)설정)의 필요성: 영지식성 확보
프로토콜 1이 약한 영지식성을 만족하는 이유는 프로토콜의 과정 1의 덕분이다. 검증자는 \(x\) 뿐만 아니라 과정 1에서 생성된 \(v\)의 값 또한 알지 못한다. 위의 약한 영지식성 문제에서 살펴보았듯이, 검증자는 \(f^-1\left( r \right)\)로부터 \(x\)를 알아내기 위해 \(v\)까지 함께 알아내야 한다. 그러나 함수 \(f\)는 injective이기 때문에 \(f^-1\left( r \right)\)에 대응되는 쌍 \(\left( v,x \right)\)가 유일하지 않다. 만약 과정 1에서 \(v\)가 고정된 값이라면, 함수 \(f\)의 domain의 원소의 개수가 \(\left( p-1 \right)\)이 되어 \(c\)값의 선택에 따라 (\(c\)와 \(p-1\)이 서로소인 경우) \(f\)가 one-to-one correspondence (bijective)가 될 수 있다. 다시 말해, \(v\)가 고정된 값이라면 \(f^-1\left( r \right)\)의 유일한 값 \(x\)가 존재 할 수 있고, 검증자가 이를 찾을 수도 있다.
-
집합 \(F_p\)는 특성(characteristic)이 \(p\)인 유한 체(finite field)이다. \(F_p:=\left\{ 0,1,\cdots ,p-1 \right\}\)이고, 모든 원소간의 더하기 및 곱하기 연산에는 \(\bmod p\)가 적용된다. \(F_p^*\)는 \(F_p\)에서 원소 0을 제외한 집합이다. ↩
-
어떤 원소 \(a\in F_p\)가 primitive element이면, \(a\)의 제곱으로 구성된 집합, 즉, \(\left\{ a^i,\forall i\in \mathbb{Z}_0^+ \right\}\)의 원소의 개수는 \(p-1\)이다. 관련 정보: https://en.wikipedia.org/wiki/Primitive_element_(finite_field) ↩
-
Fermat’s little theorem: 서로소인 \(a\)와 \(p\)에 대해, \(a^p-1\bmod p\equiv 1\). 관련 정보: https://en.wikipedia.org/wiki/Fermat%27s_little_theorem ↩
-
검증자가 건네받은 또 다른 값인 \(t\)는 \(v\)로부터 생성된 값인데, \(t\)에서 거꾸로 \(v\)를 찾는 것은 discrete logarithm 문제로써 확률이 \(\left( p-1 \right)^-1\)으로 매우 낮고, 계산적으로도 매우 어렵다. ↩
