작성자: 장재혁, GIST 블록체인 인터넷 경제 연구센터 (센터장 이흥노)

This work was created through a joint research with Onther Co., LTD., and supported by a grant-in-aid of Institute of Information & Communications Technology Planning & Evaluation (IITP), Republic of Korea.

이 글은 정보통신기획평가원(IITP)의 지원을 받아 (주)온더와의 공동연구를 통해 만들어진 결과물이다.

Groth16이란 Jens Groth가 2016년 Eurocrypt 학술대회에서 발표한 논문¹에 수록된 zk-SNARK 프로토콜이다. Groth16은 2013년 B. Parno에 의해 제안된 zk-SNARK 프로토콜인 “Pinocchio”의² 원리를 따르고 일부 성능을 개선한 프로토콜이다. 이 외에도 2020년 영국의 Aztec 그룹에서 발표된 “PlonK”도³ 원리가 비슷한 부분이 많다. 이러한 zk-SNARK 연구자들의 주요 관심사는 증명과정이 더 빠르고, 증거의 크기가 더 작으며, 검증과정이 더 빠른 프로토콜을 설계하는 것이다.

Groth16과 같은 최근 연구된 zk-SNARK 프로토콜들은 그림 5와 같이 단순하게 묘사될 수 있다.

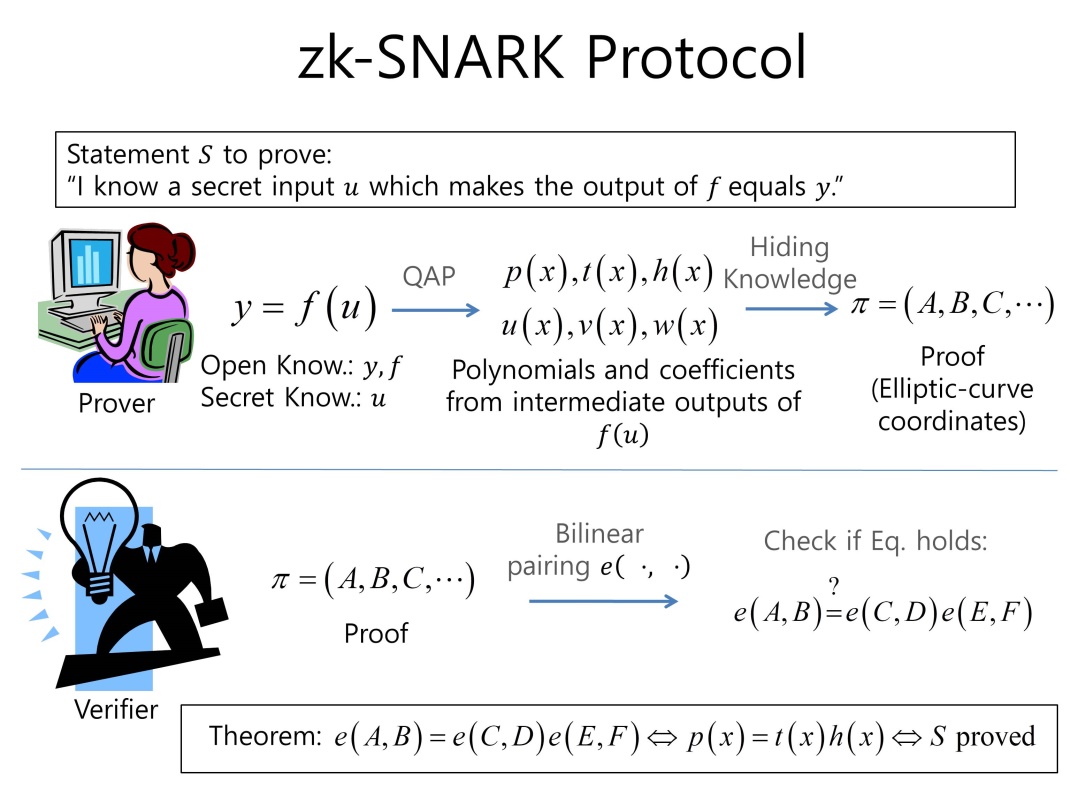그림 5 최근 zk-SNARK 프로토콜들의 작동 원리

그림 5에서의 명제 \(S\)는 “증명자는 비공개 정보 \(u\)를 알며, 이를 사용하여 함수 \(f\left( u \right)\) 충실히 계산 했고, 그 결과로 \(y\)를 얻었다”이다. 여기서 함수 \(f\)와 출력 값 \(y\)는 공개된 정보이다. 그림 5의 증명 프로토콜은 증명과정과 검증과정의 두 과정으로 구분된다. 증명과정은 \(f\left( u \right)\)의 연산과정을 분해하여 연산조각을 생성한 후, 연산조각을 암호화하여 최종 증거를 생성한다. 연산조각이란 두 개의 입력, 하나의 산술연산, 그리고 하나의 출력으로 구성된 최소 단위의 연산이다. 연산조각들이 서로 연결되면 \(f\left( u \right)\)의 연산과정 전체를 표현 할 수 있다. 즉, \(f\left( u \right)\)를 연산하는 과정에서 발생하는 모든 중간 계산값들이 연산조각들의 입력과 출력이 되는 것이다. 그러므로 오직 비공개 정보 \(u\)를 알고 있는 증명자만이 \(f\left( u \right)\)의 연산 과정을 분해 할 수 있다. 후에 검증자는 연산조각들을 건네 받아 연결 함으로써 \(f\left( u \right)\)의 연산이 올바르게 수행되었는지 확인이 가능하다. 즉, 이 과정은 증명의 완전성을 보장하는 역할을 수행한다. 이 과정을 quadratic arithmetic program(QAP)이라 한다.

그런데 이때 프로토콜의 영지식성과 건실성을 위해서 증명자는 연산조각들을 암호화 할 필요가 있다. 연산조각들을 연결하여 \(f\left( u \right)\)의 연산 과정이 알려지면 비공개 정보가 노출되기 때문이다. 그러므로 증명자는 연산조각을 암호화 하여 건네야 하며, 검증자는 암호화된 연산조각을 활용하여 \(f\left( u \right)\)의 연산 과정은 모르되 연산조각들에 오류가 없다는 것을 확인할 수 있어야 한다. 암호화에는 elliptic curve cryptography(ECC), 검증에는 pairing이라는 수학이 사용된다.