작성자: 장재혁, GIST 블록체인 인터넷 경제 연구센터 (센터장 이흥노)

This work was created through a joint research with Onther Co., LTD., and supported by a grant-in-aid of Institute of Information & Communications Technology Planning & Evaluation (IITP), Republic of Korea.

이 글은 정보통신기획평가원(IITP)의 지원을 받아 (주)온더와의 공동연구를 통해 만들어진 결과물이다.

저자는 소규모의 연산 프로그램에 대해 Groth16의 증명 프로토콜을 실습 할 수 있도록 도와주는 오픈소스 구현체를 제공하고 있다 (링크: https://codeocean.com/capsule/8850121). 구현체는 MATLAB으로 구현되었으며, 링크를 통해 MATLAB이 설치되지 않은 PC에서도 실행이 가능하다. 먼저 program analysis와 QAP 등이 어떻게 구현되었는지 살펴 본 후, 간단한 예제를 통해 프로토콜을 수행해 보는 실습을 하겠다.

구현 설명서

앞서 그림 5와 함께 살펴보았듯이, Groth16은 program analysis, QAP, ECC, 그리고 pairing의 과정을 거친다. Program analysis는 주어진 연산 프로그램 \(f\)를 연산조각들로 분해하는 과정이다. QAP는 연산조각들을 다항식과 계수의 집합으로 치환한다. 다항식과 계수를 조합하여 CRS와 증거를 생성한다. ECC는 증거를 암호화하여 증명 프로토콜의 건실성과 영지식성을 보장한다. Pairing은 증거가 암호화된 상태에서도 프로토콜이 완전성을 보장받을 수 있도록 한다.

Program analysis의 구현

프로토콜의 구성요소들 중 program analysis는 R1CS라는 방식으로 구현되었다¹. R1CS는 그림 6과 같은 써킷을 행렬연산 형태로 표현하는 것이다. 구체적으로, R1CS는 벡터 \(\mathbf{R}\)과 행렬 \(\mathbf{A}\), \(\mathbf{B}\), \(\mathbf{C}\)를 생성하고, 이들은 다음과 같은 관계를 만족한다:

여기서 연산 \(\circ\)는 Hadamard 곱, 즉 성분별 곱(elementwise product)이며, 크기가 같은 두 벡터 혹은 두 행렬에 대하여 같은 크기의 벡터 혹은 행렬을 출력하고, 출력 벡터 혹은 행렬의 성분은 같은 위치의 입력 성분끼리 곱한 결과이다. 예를 들어, \(\begin{bmatrix} 1 & 2 \end{bmatrix} \cdot \begin{bmatrix} 3 & 4 \end{bmatrix} = \begin{bmatrix} 3 & 8 \end{bmatrix}\)이다. 써킷에 존재하는 모든 곱셈 게이트에 대하여, 행렬 \(\mathbf{A}\)는 게이트의 왼쪽 입력, 행렬 \(\mathbf{B}\)는 게이트의 오른쪽 입력, 행렬 \(\mathbf{C}\)는 게이트의 출력이 기록되어 있으며, 행렬의 서로 다른 게이트의 정보는 서로 다른 열에 기록된다. 벡터 \(\mathbf{R}\)에는 써킷의 모든 곱셈 게이트의 중간 계산 값들이 기록된다. 즉, \(\mathbf{R}\)의 값들이 Groth16 프로토콜에서 사용되는 QAP 계수들 \(c_i\)이다. 따라서 각 행렬들의 크기는 \(m \times n\)이다. 예를 들어, \(f:C_6 = (C_1 + C_2 )C_3 C_4\)에 대응되는 써킷은 다음과 같은 R1CS 형태로 표현될 수 있다:

식 (2)를 계산 해 보면, 첫 번째 열은 \(C_3 C_4 = C_5\)를 표현하며, 두 번째 열은 \(( C_1 + C_2 ) C_5 = C_6\)을 표현하기 때문에 \(\mathbf{R}\), \(\mathbf{A}\), \(\mathbf{B}\), \(\mathbf{C}\)가 \(f\)의 한 써킷을 대변한다고 말할 수 있다. 한편, 주어진 연산 프로그램 \(f\)에 대하여, 써킷의 형태가 다양 할 수 있는 것과 마찬가지로 R1CS의 결과도 다양할 수 있다. 예를 들어, \(f\)는 다음과 같은 R1CS로써 표현될 수도 있다:

식 (2)의 R1CS와 식 (3)의 R1CS는 모두 \(f:C_6 = ( C_1 + C_2 ) C_3 C_4\)라는 같은 연산프로그램을 다르게 표현 한 것이다 (\(C_7, C_8, C_9, C_10\)은 중간 계산 값이다).식 (3)의 R1CS는 식 (2)의 R1CS에 비해 행과 열의 개수가 더 많다. R1CS의 행의 개수는 써킷에 존재하는 선의 개수와 같으며, 열의 개수는 써킷에 존재하는 곱셈 게이트의 개수와 같다. 이전의 분석을 통해 써킷의 선과 곱셈 게이트가 많을수록 증거의 길이가 길어짐을 확인하였다. 따라서 식 (2)의 R1CS가 식 (3)보다 더 간결한 증거를 야기한다.

QAP의 구현

Program analysis (R1CS) 이후 QAP과정을 거쳐 다항식을 생성한다. QAP는 써킷의 구조를 다항식의 형태로 저장하는 것인데, 이전의 R1CS에서 이미 써킷의 구조를 행렬의 형태로 저장해 놓았다. 행렬 \(\mathbf{A}\),\(\mathbf{B}\),\(\mathbf{C}\)가 바로 그것이다. 따라서 QAP과정에서 해야 할 일은 행렬 \(\mathbf{A}\),\(\mathbf{B}\),\(\mathbf{C}\)를 다항식으로 변환하는 것이다. 먼저 임의의 근(root)들을 설정 한 후, 근 다항식 \(t ( x )\)을 정의한다. 근의 개수는 R1CS 행렬의 열 개수와 일치하도록 정한다. 이제 행렬 \(\mathbf{A}\),\(\mathbf{B}\),\(\mathbf{C}\) 각각의 행을 다항식으로 변환한다. 다항식의 입력 변수를 \(x\) 출력 변수를 \(y\)라 할 때, 각각의 행의 성분들이 \(y\)의 표본이 되고, 근 다항식의 근들이 \(x\)의 표본이 되도록 설정한다. 이렇게 정의한 표본을 바탕으로 보간법을 수행하여 연속형태의 다항식을 생성한다. 이 과정을 모든 행렬의 모든 \(3m\)개의 행에 대하여 반복하여 총 \(3m\)개의 다항식을 보간법으로 생성한다. 예를 들어, 식 (2)의 R1CS인 경우 근의 개수는 2개이며, 각각의 근을 \(r_1 = 1\), \(r_2=2\)와 같이 설정 할 수 있다. 그러면 근 다항식은 \(t ( x ) = ( x-1 ) ( x-2 )\)가 된다. 예를 들어 행렬 \(\mathbf{B}\)의 네 번째 행에 대응되는 다항식을 생성하는 경우, 표본은 \(( 1,1 ), ( 2,0 )\)이며, 이 두 개의 표본을 바탕으로 보간법을 수행한다.

보간법은 선형대수를 사용하여 수행 할 수 있다. 번호 \(i=1,\cdots ,n\)에 대하여 근 다항식의 근을 \(r_i\)라 명명하겠다. 여기서 근의 개수는 써킷의 곱셈 게이트의 개수 \(n\)과 같다. 어떤 QAP 다항식 \(y = a_0 + a_1x + a_2 x^2 + \cdots + a_n-1 x^{n-1}\) 에 대해 \(n\)개의 보간 표본이 \(( r_1, y_1 ), ( r_2, y_2 ), \cdots, ( r_n, y_n )\)일 때, 표본의\(x\)성분 과 \(y\)성분 사이에는 다음과 같은 선형 관계가 성립된다:

이때 전달행렬 \(\mathbf{V}\)가 Vandermonde 행렬²이라는 특수한 형태가 되고, Vandermonde 행렬은 항상 역행렬이 존재한다. 이제 연속 다항식의 계수 \(a_0, \cdots ,a_n\)을 찾는 보간법은 다음의 선형 역문제를 푸는 것이다:

근 다항식의 근 \(r_i\)는 \(i=1,\cdots ,n\)에 대해 서로 다르기만 하다면 임의로 설정하여도 문제가 없지만, 보간법을 더 계산효율적으로 수행하기 위해 특수하게 설정하는 경우도 있다. 전달행렬 \(\mathbf{V}\)는 특수성으로 인해 언제나 역행렬 \(\mathbf{V}^{-1}\)가 존재하기는 하지만, \(\mathbf{V}^{-1}\)를 계산하는 것은 여전히 많은 계산 량을 필요로 한다. 계산 량을 줄이기 위해, 다항식의 근을 적절히 설정하여 행렬 \(\mathbf{V}\)를 DFT 행렬로 만들 수 있다. DFT행렬이란 Vandermonde 행렬의 특수한 경우로, \(k,l\)번째 성분이 \(e^{j 2 \pi \frac{kl}{n}}\)인 행렬이다. 근 다항식의 근들을 \(i=1,\cdots ,n\)에 대해 \(r_i = e^{j 2 \pi \frac{i}{n}}\)로 설정하면 \(\mathbf{V}\)를 DFT 행렬로 만들 수 있다. 여기서 \(j = \sqrt{-1}\)는 허수이다. \(\mathbf{V}\)가 DFT 행렬이 되면 좋은 점은 fast Fourier transform(FFT)³ 알고리즘을 사용 할 수 있게 된다는 것이며, 그러면 의 역문제를 \(O\left( n\log n \right)\)이라는 아주 적은 계산 량으로 풀 수 있다.

ECC의 구현

MATLAB 구현체에서 ECC를 위해 사용하는 타원곡선은 \(E:y^2 = x^3 + x\)이며, \(x\)와 \(y\)는 유한 체 \(F_p\)에서 정의되었다. 여기서 체의 크기는 \(p=71\)이다. 이렇게 정의된 타원곡선 \(E\)는 supersingular 타원곡선⁴이라 불리며, pairing에 유리한 특성을 가지고 있다.

타원곡선 \(E\)를 pairing에 조금 더 유리하게 사용하기 위해서 확장 체 (extension field)의 개념을 함께 사용한다. 유한 체 \(F_p\)의 order가 2인 확장 체는 \(F_{p^2}\)으로 표기된다. 한 예로, 확장체는 \(F_p\)의 원소에 허수인 \(j=\sqrt{-1}\)의 사용을 허용함으로써 확장 가능하다. 예를 들어, \(F_3=\left\{ 0,1,2 \right\}\)의 확장 체는 \(F_{3^2} = \left\{ 0, 1, 2, j, j2, 1+j, 1+j2, 2+j, 2+j2 \right\}\)일 수 있다. 만약 \(F_p \times F_p\)의 한 원소인 \(\left( x, y \right)\)가 타원곡선 \(E\)상의 한 점이라면, \(\left( -x, jy \right)\)또한 타원곡선 \(E\)상의 한 점인 것을 알 수 있다. 그리고 그 점 \(\left( -x, jy \right)\)는 \(F_{p^2} \times F_{p^2}\)의 한 원소라는 것을 알 수 있다. 다시 말하면, \(F_p\)상에서 정의된 \(E\)의 점들을 \(F_{p^2}\)으로 확장하는 것은 간단히 수행 가능하다.

Groth16의 증명 프로토콜에서는 타원곡선 \(E\)의 점들 중 두 개의 generator인 \(G\)와 \(H\)를 사용한다. MATLAB 구현체에서도 \(G\)와 \(H\)를 사용하며, pairing에 유리하도록 사용하기 위해 \(G\)와 \(H\)가 다음과 같은 관계가 되도록 선택하였다: \(G\)는 타원곡선 \(E\)의 generator들 중 임의로 선택되었다: \(G = \left( x_G, y_G \right)\)라 할 때, \(H = \left( -x_G, jy_G \right)\)이다. 따라서 \(G\in F_p\)이고 \(H \in F_{p^2}\)이다.

Pairing의 구현

Pairing은 Weil pairing을 구현하였다. 다른 pairing들인 Ate pairing, Tate pairing도 모두 Weil pairing의 계산원리에서 조금만 변형하면 구현이 가능하다. Weil pairing은 D. Boneh와 M. Franklin의 논문인 “Identity-based encryption from the Weil pairing”⁵의 Appendix에 기술된 정의와 계산 방법을 그대로 사용하여 구현하였다. 이 때, 효율적인 계산을 위해 Miller algorithm⁶이 사용된다. 특이사항으로, \(O \left( p^{-1} \log p \right)\)의 확률로 pairing에 실패 할 수 있다. 그러나 \(p\)가 커질수록 이 확률은 매우 작아져서 실용적인 환경에서는 실패 하는 경우가 거의 없고, 만약 실패하더라도 다시 시도하면 된다.

Groth16 증명 프로토콜 사용 예제

그림 9은 MATLAB으로 구현된 Groth16 프로콜의 실행 결과이다. 연산 프로그램은 \(f:y=\left( c_1 + c_2 \right)\left( c_1 - 4 \right)\)이다. 비공개 정보는 \(c_1 = 2\)과 \(c_2 = 4\)이다. Program analysis (R1CS) 결과로 6개의 써킷 선과 3개의 곱셈 게이트가 형성되었다. R1CS의 결과를 토대로 QAP 다항식들과 복원 다항식 \(p \left( x \right)\), 몫 다항식 \(h \left( x \right)\)를 성공적으로 생성하였다. 보안 파라미터와 QAP 결과를 종합하여 CRS와 증거를 성공적으로 생성하였고, CRS의 길이는 \(3n+m+5=20\)이며, 증거의 길이는 \(3\)이다. CRS와 증거를 사용하여 검증이 성공적으로 수행되었다.

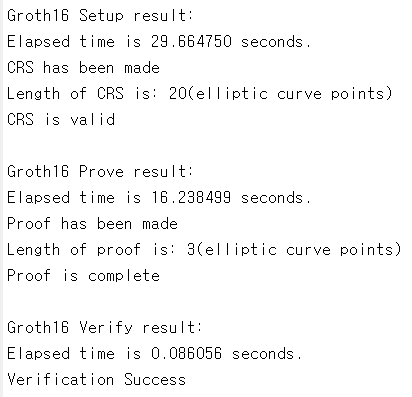그림9 MATLAB으로 구현된 Groth16 증명 프로토콜의 실행 결과

R1CS의 결과로 생성된 행렬 \(\mathbf{A}\), \(\mathbf{B}\), \(\mathbf{C}\)와 벡터 \(\mathbf{R}\)은 각각 다음과 같다:

그림 10 R1CS로 생성된 행렬 A,B,C와 벡터 R

그림 10에서 생성된 \(\mathbf{R}\)은 \(\mathbf{R} ( c_1, c_2 ) = \left[ 1, c_1, c_2, c_3 = c_1 c_2, c_4 = c_1^2, y = -4 c_2 - 4 c_1 + c_3 + c_4 \right]\)에 각각 \(c_1 = 2\)와 \(c_2 = 4\)를 대입한 결과이다. \(\mathbf{R}\left( c_1, c_2 \right)\)와 행렬 \(\mathbf{A}\), \(\mathbf{B}\), \(\mathbf{C}\)를 사용하여 식 (1)을 계산한 후 왼쪽 열부터 읽으면 다음의 관계식들을 순서대로 얻을 수 있다:

관계식 (6)은 연산 프로그램 \(f:C_6 = \left( C_1 + C_2 \right) C_3 C_4\)와 일치하므로, R1CS가 성공적으로 수행되었음을 알 수 있다.

QAP를 수행하기 위해, 근 다항식 \(t\left( x \right)\)의 근을 \(r_1 = 1\), \(r_2 = 2\), \(r_3 = 3\)으로 설정하였다. 따라서 \(t\left( x \right) = \left( x-1 \right)\left( x-2 \right)\left( x-3 \right)\)이다. 행렬 \(\mathbf{A}\)의 두 번째 행에 대응되는 다항식, 즉 \(w_2\left( x \right)\)의 표본은 \(\left( 1,1 \right), \left( 2,1 \right), \left( 3, -4 \right)\)이며, 보간법을 적용한 결과는 \(w_2\left( x \right)=-2.5 x^2 + 7.5 x - 4\)로 계산되었다. 마찬가지로, 행렬 \(\mathbf{C}\)의 4번째 행에 대응되는 다항식, 즉 \(y_4\left( x \right)\)의 표본은 \(\left( 1,0 \right), \left( 2,0 \right), \left( 3,0 \right)\)이며, 보간법을 적용한 결과는 \(y_4\left( x \right) = 0.5 x^2 - 1.5 x + 1\)로 계산되었다. 이러한 방법으로 \(i=1,\cdots ,6\)에 대하여 모든 다항식 \(w_i\left( x \right)\), \(v_i\left( x \right)\), \(y_i\left( x \right)\)를 생성하였다 (그림 11). 이를 토대로 \(p\left( x \right)\)를 계산하였고, 마지막으로 \(h\left( x \right) = p\left( x \right) / t\left( x \right)\)를 계산하였다. \(p\left( x \right)\)에 \(k=1,\cdots ,3\)에 대하여 \(x = r_k\)를 대입한 후 \(p\left( r_k \right) = 0\)임을 확인하여 QAP의 결과가올 바른지 확인하였다 (그림 12).

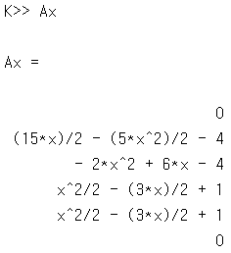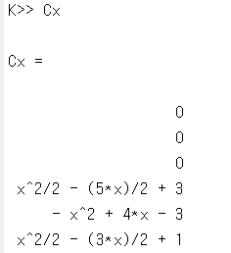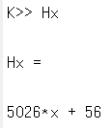그림 11 QAP 왼쪽부터 다항식 \(w_i\left( x \right)\), \(v_i\left( x \right)\), \(y_i\left( x \right)\)와 몫 다항식 \(h\left( x \right)\)의 계산 결과. 행렬 \(\text{Ax}\) 와 \(\text{Bx}\), \(\text{Cx}\)의 첫 번째 행부터 마지막 행까지 순서대로 \(i=1,\cdots ,6\)에 대응된다.

그림 12 복원 다항식 \(p\left( x \right)\)가 올바르게 생성되었는지 확인하는 코드

한편 MATLAB으로 구현한 Groth16 프로토콜의 QAP는 유한 체 \(F_q\)에서 작동한다. 여기서 \(q=p^2-1\)이다⁷. 따라서 QAP 다항식들의 계수들이 \(F_q\)의 원소여야 한다. 따라서 \(i=1,\cdots ,6\)에 대한 모든 다항식 \(w_i\left( x \right)\), \(v_i\left( x \right)\), \(y_i\left( x \right)\)의 계수들에 존재하는 유리수들을 정수로 변환하기 위해 임의의 상수 \(u\)를 사용 할 수 있다. 이때 \(u\)는 모든 계수들의 분모의 최소 공배수이다. QAP의 완전성을 위한 관계식인 \(( \sum\nolimits_{i=1}^{6} c_i w_i ( x ) ) \cdot ( \sum\nolimits_{i=1}^{6} c_i v_i( x ) ) - ( \sum\nolimits_{i=1}^{6} c_i y_i ( x ) ) = h ( x ) t ( x )\)의 관계를 유지하면서 다항식의 계수들을 정수로 변환하는 방법은 \(w_i ( x ) \leftarrow u w_i ( x )\), \(v_i( x ) = u v_i ( x )\), \(y_i ( x ) = u^2 y_i ( x )\), \(h ( x ) \leftarrow u^2 h ( x )\)로 변환하는 것이다. 이렇게 하면

이 되어 QAP의 완전성이 유지된다.

그림 13 유리수 계수들의 분모의 최소공배수를 곱하여 계수를 정수로 변환하는 코드

QAP 결과를 ECC로 암호화하기에 앞서, 먼저 타원곡선의 두 generator로 사용될 \(G\)와 \(H\)를 선택하였다. \(G\)의 좌표는 \(( 11,8 )\)이고, \(H\)의 좌표는 \(( -11 \bmod 71,j8\bmod 71 ) = t ( 60,j8 )\)이다 (그림 14). 타원 곡선의 모든 점과 각 점의 특성은 링크 https://graui.de/code/elliptic2/> 에서 확인 할 수 있으며, MATLAB 구현체에서도 주어진 타원 곡선의 모든 점을 찾는 함수(EC_points.m)와 generator를 찾는 함수(EC_order.m)가 제공된다.

그림 14 Generator G와 H

준비된 QAP 결과와 타원곡선을 사용하여, Groth16 프로토콜의 Setup, Prove, Verify를 순서대로 수행한다. Setup과정과 Prove과정에서 선택되는 파라미터인 \(\tau\)와 \(r, s\)는 매번 무작위로 선택되도록 설계되었다. Setup 과정에서 CRS 데이터인 길이 14의 \(\sigma_G\)와 길이 6의 \(\sigma_H\)를 생성하며, 구현체에서는 \(\sigma_G\)가 sigma1_1, sigma1_2, …, sigma1_5에, 그리고 \(\sigma_H\)가 sigma2_1, sigma2_2에 분리되어 저장된다. Prove 과정에서는 길이 3의 증거 \(\pi\)를 생성하며, 구현체에서는 proof로 명명되었다. Verify 과정에서 계산되는 \(LHS\)와 \(RHS\)는 모두 \(F_p\)의 원소이며, \(LHS=RHS\)임을 확인하여 최종 검증결과를 출력한다.

최종 검증결과는 그림 9와 같으며, Groth16 프로토콜의 모든 과정이 성공적으로 수행되었음을 알 수 있다.